Hausuebung_Sudoku.html

Hausübung 4b: Programmierung (15 Punkte, Abgabe bis 25.6.10)

Einfache Sudokus

(a)
Schreiben Sie eine Prozedur, die für ein Sudokurätsel X für jedes unbesetzte Feld die Menge der möglichen Kandidaten für dieses Feld zurückgibt.

X soll als 9 × 9-Matrix oder -Array übergeben werden, wobei die unbesetzten Felder mit 0 kodiert sind.

(b)
Schreiben Sie eine Prozedur, die ein Sudokorätsel schön formatiert (wie üblich) ausgibt. Mit einem optionalen Argument soll man statt der freien Felder die dort möglichen Zahlen angezeigt bekommen; siehe (a).

(c)

Schreibe ein Löser für einfache Sudokus. Das sollen solche sein, die sich nur durch Einsetzen der eindeutigen Kandidaten lösen lassen. Falls das nicht geht oder falls es keine Lösung gibt (null Möglichkeiten für ein leeres Feld), soll eine entsprechende Meldung ausgegeben werden.

______________________________________________________

Ein vollständiger Löser, z.B. mit backtracking, ist nicht verlangt.

> restart;

> with(plots):

> X:=Matrix([[ 8 , 4 , 3 , 0 , 0 , 0 , 2 , 5 , 9 ],
       [ 6 , 7 , 9 , 2 , 0 , 5 , 8 , 3 , 1 ],
       [ 0 , 0 , 2 , 9 , 0 , 3 , 7 , 0 , 0 ],
       [ 0 , 0 , 0 , 7 , 0 , 2 , 0 , 0 , 0 ],
       [ 5 , 0 , 6 , 4 , 0 , 9 , 1 , 0 , 7 ],
       [ 0 , 0 , 0 , 6 , 0 , 8 , 0 , 0 , 0 ],
       [ 0 , 0 , 7 , 3 , 0 , 4 , 5 , 0 , 0 ],
       [ 3 , 6 , 8 , 5 , 0 , 7 , 9 , 1 , 4 ],
       [ 4 , 9 , 5 , 0 , 0 , 0 , 3 , 7 , 2 ]]):

Aufgabe a) -Alle Möglichkeiten für ein Feld

> Moeglichkeiten:=proc(Sudoku,zeile::integer,spalte::integer)
local Spalte,Zeile,i,block3x3,ergebnis;
Spalte:=NULL;Zeile:=NULL;
if Sudoku[zeile,spalte]>0 then "In dieses Feld ist bereits eine Zahl eingetragen" else
     for i from 1 to 9 do
       Zeile:=Zeile,Sudoku[zeile,i];
       Spalte:=Spalte,Sudoku[i,spalte];
     end do;
  block3x3:={seq(Sudoku[floor((zeile - 1) / 3) * 3 + (k mod 3) +1,
  floor((spalte - 1) / 3) * 3 + floor(k / 3)+1],k = 0..8)};

  ergebnis:=({seq(i,i=1..9)} minus {Zeile}) intersect ({seq(i,i=1..9)} minus {Spalte})
  intersect ({seq(i,i=1..9)} minus block3x3 );

end if;
return ergebnis;
end proc:

Kommentar: Die Prozedur gibt zu einem bestimmten Feld von der "Sudoku-Matrix" (Zeile,Spalte) die möglichen Kandidaten für dieses Feld aus. Ist das Feld bereits "besetzt" wird ein entsprechender Hinweis ausgegeben. Die möglichen Kandidaten werden ermittel über die Schnittmenge Dabei ist M die Menge der Zahlen von 1..9,die Menge der Zahlen in der entsprechenden Zeile, in der entsprechenden Spalte und die Menge der Zahlen in dem jeweiligen 3x3 Block. Die möglichen Kandidaten errechnen sich somit über die Schnittmenge der fehlenden Zaheln in Zeile, Spalte und 3x3 Block. Dabei werden die Zahlen in dem 3x3 Block ermittelt mit floor- und mod-Befehlen. Denn (floor(zeile-1)/3)*3 ergibt 0 für zeile<4, 3 für 3<zeile<7 und 6 für zeile>6. ((k mod 3) +1) ergibt in einer Sequenz immer wieder die Zahlenfolge (1,2,3). Man durchläuft also den 3x3 Block von "oben nach unten", also immer eine Zeile weiter bei gleichbleibender Spalte und nach 3 Zeilen beginnt mit man wieder von vorne mit der nächsten Spalte usw.
Ergebnis:

> Moeglichkeiten(X,3,2);

(1)

Aufgabe b) Sudokuplot

> freebox:=proc(Sudoku)
# Die Prozedur freebox gibt eine Liste in der Form [Zeile,Spalte],[Zeile,Spalte]... der unbesetzten Felder zurück
local i,k,L2;
L2:=NULL;
for i from 1 to 9 do
  for k from 1 to 9 do
    if Sudoku[i,k]=0 then L2:=L2,[i,k]; fi;
  end do;
end do;
return L2;
end proc:

> Sudokuplot:=proc(Sudoku,zeigeKandidaten)
local Sneu,i,P,T,T2;
Sneu:=copy(Sudoku):
if is(nops([freebox(Sudoku)]),'positive')=true then
          #Matrix die 0en durch Leerzeichen ersetzt, für leere Felder in der Grafik
          for i from 1 to 81 do
            if Sneu(i)=0 then Sneu(i):="" fi;
          end do:
               if zeigeKandidaten=true then
                 T2:=textplot([seq([0.45+freebox(Sudoku)[i][2]-1,8.18-freebox(Sudoku)[i][1]+1,
                 Moeglichkeiten(Sudoku,freebox(Sudoku)[i][1],freebox(Sudoku)[i][2])],
                 i=1..nops( [freebox(Sudoku)]))],font = [TIMES, ROMAN, 7]):
               else T2:=plot(0,x=0..9,color=black);
               end if;
else T2:=plot(0,x=0..9,color=black);
end if;

#Eigentliches Sudoku-Feld (P) + Zahlen (T)
P:=plot([seq([[i,0],[i,9]],i=0..9),seq([[0,9-i],[9,9-i]],i=0..9)],thickness = [1, 1, 1, 2, 1, 1, 2, 1, 1, 1, 1, 1, 1, 2,1,1,2], color = black,axes=none):
T := textplot([seq(seq([0.48+k,8.45-i,Sneu(k*9+i+1)],i=0..8),k=0..8)], font = [TIMES, ROMAN, 17]):
display(P,T,T2);
end proc:

Die Funktion Sudokuplot zeichnet das Sudoku. Dabei wird zuerst abgefragt ob es überhaupt unbesetzte Felder gibt. Wenn es welche gibt, werden in einer Kopie der "Sudoku-Matrix" X die Nullen durch Leerzeichen ersetzt. Wenn zudem Kandidaten eingetragen werden sollen, wird dies durch einen Textplot und der Prozedur aus Aufgabe a) realisiert. Das Sudoku-Feld an sich wird einfach durch horizontale und senkrechte Geraden geplottet.
Ergebnis:

> Sudokuplot(X,true);
Sudokuplot(X,false);

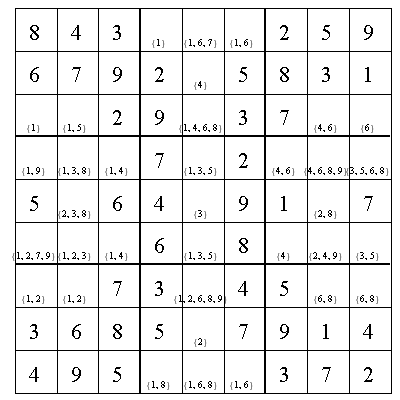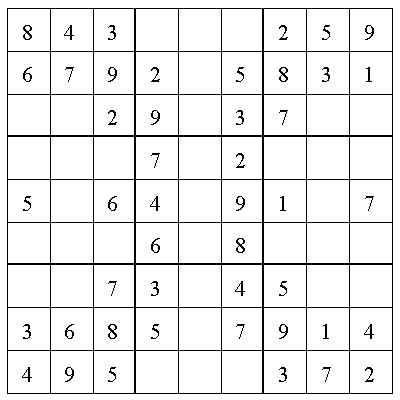Plot_2d

Plot_2d

Aufgabe c) Lösung des Sudokus

> Sudokuloeser:=proc(Sudoku)
local i,k,j,loes,a;
loes:=copy(Sudoku);i:=1;
    while i=1 do
    i:=2;
     for k from 1 to 9 do
      for j from 1 to 9 do
       a:=Moeglichkeiten(loes,k,j):
        if loes[k,j] = 0 and nops(a)=1 then
        loes[k,j]:=op(1,a);i:=1;
        elif loes[k,j]=0 and nops(a)=0 then
        printf("Dieses Sudoku ist nicht lösbar!");return;
        end if;
      end do;
     end do;
    end do;
if is(nops([freebox(loes)]),'positive')=false then
   printf("Das Sudoku konnte gelöst werden: %d Felder wurden gefüllt.", nops([freebox(Sudoku)]));
   Sudokuplot(loes,false);
else printf("Das Sudoku konnte nicht vollständig gelöst werden, da es zu schwer zu lösen ist!");
fi;
end proc:

Kommentar: Die Idee hinter dem Sudokulöser ist es, das Sudoku Feld für Feld durchzugehen und zu schauen ob es eindeutige Kandidaten gibt. Sollte es welche geben, werden diese eingetragen, und das Sudoku wird mit neu berechneten Kandidaten wieder auf eindeutige Kandidaten geprüft usw. Dies wird realisiert durch zwei for-Schleifen, die jede Zeile und Spalte "Feld für Feld" abfragen und einer while Schleife, die dafür sorgt, dass das Sudoku immer wieder durchlaufen wird, sollte es noch freie Felder geben (i wird wieder 1 gesetzt um die while Schleife erneut zu durchlaufen). Sollte es für ein leeres Feld 0 Kandidaten geben (nops(a)=0) ist das Sudoku nicht lösbar und ein Hinweis wird ausgegeben. Sobald die while-Schleife "beendet" wurde, wird noch überprüft ob alle Felder ausgefüllt sind. Ist das nicht der Fall, war das Sudoku zu schwer!

> Sudokuloeser(X);

Das Sudoku konnte gelöst werden: 35 Felder wurden gefüllt.

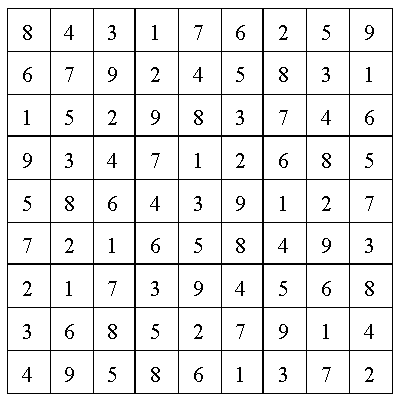Plot_2d

> X2:=copy(X):X2[7,1]:=1:Sudokuloeser(X2);

Dieses Sudoku ist nicht lösbar!

> X2:=Matrix([[ 0 , 0 , 0 , 5 , 8 , 9 , 0 , 0 , 6 ],
       [ 0 , 0 , 5 , 0 , 0 , 3 , 0 , 2 , 0 ],
       [ 0 , 6 , 0 , 0 , 0 , 1 , 5 , 0 , 0 ],
       [ 0 , 0 , 8 , 0 , 0 , 0 , 0 , 0 , 3 ],
       [ 0 , 1 , 0 , 0 , 6 , 0 , 0 , 9 , 0 ],
       [ 7 , 0 , 0 , 0 , 0 , 0 , 1 , 0 , 0 ],
       [ 0 , 0 , 7 , 4 , 0 , 0 , 0 , 1 , 0 ],
       [ 0 , 5 , 0 , 7 , 0 , 0 , 9 , 0 , 0 ],
       [ 2 , 0 , 0 , 1 , 3 , 6 , 0 , 0 , 0 ]]):

> Sudokuloeser(X2);

Das Sudoku konnte nicht vollständig gelöst werden, da es zu schwer zu lösen ist!

Alternativ kann man bei a) natürlich auch alle Kandidaten auf einmal in eine Matrix ausgeben:

Matrix(%id = 106898172) (2)